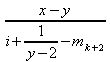
Nun hat das W3-Consortium auch noch MathML verabschiedet, was zu einer wahren Inflation von mathematischen Ausdrücken führen wird, die es in Programme umzusetzen gilt. Nachdem sich auch die gängigen Systeme für Computer Algebra auf MathML umstellen und OpenOffice ausschließlich MathML unterstützt, sollte Java nachziehen.
Hier werden die nötigen Grundlagen erarbeitet. Das Ziel ist es, diese beiden Systeme miteinander zu verbinden und MathML-Sequenzen in lauffähige Java-Programme zu übersetzen. Dieser Abschnitt zeigt, wie aus dem in MathML verfassten Ausdruck
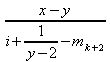
die Java-Sequenz
(x-y)/(i+1/(y-2)-m[k+2])
wird. Natürlich können hier nur die elementaren Gegebenheiten besprochen werden, jedoch dürfte das Potenzial der Kombination MathML / Java schnell offenbar werden.
In diesem Programm wird der DOM-Parser eingesetzt, weil hier der gesamte Baum des Dokuments im Arbeitsspeicher vorhanden ist. Natürlich können auch eigene Strukturen benutzt werden, aber bislang fehlte sowieso ein DOM-Beispiel. An der prinzipiellen Berabeitung ändert sich nicht das Geringste. Wesentlich ist eine Baumstruktur; ob mit SAX-Parsing mit eigenem binary tree oder mit DOM-Parsing und dem dort vorhandenen Baum.
In der main-Sequenz sind nur zwei Stellen für den Übersetzungsvorgang verantwortlich. Die erste stellt das Dokument in Form eines binary trees bereit.
... DocumentBuilderFactory factory = DocumentBuilderFactory.newInstance(); DocumentBuilder builder = factory.newDocumentBuilder(); document = builder.parse( file); |
Diese Sequenz ist in eine try-catch-Struktur eingebettet, in der eventuelle Exceptions abgefangen werden. War der DOM-Parsing-Vorgang erfolgreich, steht der Baum bereit.
Die zweite Stelle
preOrder( document.getElementsByTagName( "math").item( 0)); |
besteht nur im Aufruf der Methode preOrder, der als Argument ein Teil des Baums übergeben wird. Die Methode getElementsByTagName übergibt eine Node-List des Dokuments, beginnend mit einem "math"-Tag. Von dieser Liste erwartet die Methode preOrder ein Element, bei dem es sich um das erste handeln sollte "item( 0)".
Die Umsetzung erfolgt über ein pre-order-traversal, also
handle( node)
Inhalt des Nodes bearbeiten,
preOrder( node.getFirstChild())
dann rekursiver
Aufruf für Child-Nodes,
finish( node)
Abschlußbearbeitung des
Child-Nodes und schließlich
preOrder( node.getNextSibling())
rekursiver Aufruf
für den nächsten Node innerhalb der Ebene.
Diese vier Punkte sind in der Methode
static public void preOrder( Node node) {
if (node == null) return;
handle( node); // Inhalt des Nodes bearbeiten
level++;
preOrder( node.getFirstChild()); // rekuriv Stufe hinunter steigen
level--;
finish( node); // Nachberarbeitung
preOrder( node.getNextSibling()); // rekuriv folgenden Node
}
|
farblich hervorgehoben. Zwei Punkte sind rekursive Aufrufe, wodurch sich die weitere Beschreibung auf die beiden Methoden handle und finish beschränkt.
Hier erfolgt die eigentliche Bearbeitung des aktuellen MathML-Tags. Im Vordergrund steht die Isolation der Inhalte von den elementaren Tags wie mn, mi und mo. Alles weitere wird an die Methode finish delegiert.
static public void handle( Node node) {
String name = node.getNodeName();
if (name.equals( "#text")) return;
if (name.equals( "mi")) { mi( node); return; }
if (name.equals( "mn")) { mn( node); return; }
if (name.equals( "mo")) { mo( node); return; }
if (str.length() > 0)
{
stack.push( str);
str = "";
}
stack.push( name);
}
|
Die drei Tags erhalten Methoden gleichen Namens, in denen einfach der Inhalt des Tags (NodeValue) auf dem Stack abgelegt wird. War das der Fall, wird die Methode sofort verlassen.
War kein elementares Tag vorhanden, wird globale Stringreferenz auf Vorhandensein überprüft und ggf. ebenfalls auf dem Stack abgelegt. Dieser String wird erst in der Methode finish belegt, weshalb er hier irrelevant ist. Erst jetzt wird der TagName abgelegt. Auf dem Stack ist also nur die postfix-Variante eines gruppierenden Tags vorhanden, mit dem jeweils aktuellen Tag an oberster Position.
Die einzelnen Abschnitte dieser Methode werden in verschiedenen Sequenzen besprochen. Hier gleich die erste. Liegt ein elementares Tag vor, ist diese Methode auch schon beendet. Erst bei gruppierenden Tags ist Funktionalität gefordert.
static public void finish( Node node) {
String name = node.getNodeName();
if (name.equals( "mi") ||
name.equals( "mn") ||
name.equals( "mo") ||
name.equals( "#text")) return;
|
Handelt es sich bei dem aktuellen Tag um die einfache Gruppierung, liegen alle Elemente der Gruppierung auf dem Stack. Die Methode handle hat sie hier abgelegt, so dass sie nur noch zusammengefasst werden müssen. Diese Zusammenfassung muss dann natürlich wieder auf dem Stack abgelegt werden.
if (name.equals( "mrow"))
{
while (!((String)stack.peek()).equals( name))
str = ((String)stack.pop()).concat( str);
stack.pop(); // mrow vom Stack entfernen
stack.push( str); // aufgebauten String ablegen
str = ""; // String leeren
return;
}
|
Alle Elemente zwischen "<mrow>" und "</mrow>" wurden in der while-Schleife vom Stack entfernt und zu einem String zusammengefasst. Dieser String wird dann wieder auf dem Stack abgelegt. Danach wird die Methode verlassen, denn die Gruppierung ist abgeschlossen.
Eine komplexere Gruppierung scheint "mfrac" zu sein, zumindest hat es oft im MathML-Dokument den Anschein. Dem ist jedoch keinesfalls so, wie folgende Sequenz zeigt:
if (name.equals( "mfrac"))
{
String nom = (String)stack.pop(); // Zähler
String den = (String)stack.pop(); // Nenner
/*------------------------------------------*/
/* Test, ob mfrac-Tag korrekt abgeschlossen */
/*------------------------------------------*/
str = (String)stack.pop();
if (!str.equals( "mfrac"))
{
System.out.println( "Fehlerhafter Aufbau eines Bruchterms");
System.exit( 1);
}
str = "";
/*---------------------------------*/
/* Eventuelle Summenterme klammern */
/*---------------------------------*/
if (sumTerm( nom)) nom = "(".concat( nom).concat( ")");
if (sumTerm( den)) den = "(".concat( den).concat( ")");
stack.push( den+"/"+nom);
return;
}
|
Damit sind die prinzipiellen Arbeiten zur Überführung eigentlich abgeschlossen, wären da nicht "versteckte" Klammern. Mathematiker nutzen die bildliche Darstellung von Formeln, um auf Klammern zu verzichten. ist auf oder unter einem Bruchstrich eine Summe, so ersetzt ihnen die Länge des Bruchstrichs die Klammern. Einer Programmsequenz fehlt diese Visualisierung, weshalb die Methode "sumTerm" vorhanden ist.
Diese Methode ist im Programm vorhanden und denkbar einfach. Ist im String (Zähler und/oder Nenner) eine Multiplikation oder Division so liegt immer dann ein Summenterm vor wenn vorher eine Addition oder Subtraktion gefunden wurde. Diese Überprüfung erfolgt nur in der obersten Klammerebene.
Mit einfachen Übersetzungen ist es leider nicht getan. Viele Formeln enthalten indirekt Typisierungen, die bei Mathematikern erst einmal Zahlenmengen sind. Außerdem muss zwischen Definitons- und Wertebereich unterschieden werden. Auch Schleifen werden in Formeln untergebracht, als seien es einfache Operanden.
Aus den eben genannten Gründen, die sich beliebig erweitern lassen, ein paar Anregungen zur Vereinfachung. Viele Irritationen lassen sich vermeiden, wenn ein mathematisch korrekter Ansatz vorliegt.
Mathematiker sind hemmungslos in ihrer Art, Laufanweisungen zu formulieren. Ihnen genügt ein Operator, der einfach mit sub- und sup-Termen versehen wird und fertig ist die Schleife. Die disjunktive Verknüpfung indizierter boolescher Variablen xi wird formuliert als
Das System sollte nun eine Sequenz erzeugen, die zwar eine Methode darstellt, aber nicht als Funktion sondern als Substitution anzusehen ist:
boolean op_or( long i; long k, boolean[x]) {
boolean loc = false;
for( ; i<=k; i++) loc |= x[i];
return loc;
}
|
Das funktioniert mit allen binären Operatoren (solche mit zwei Operanden). Werden spezielle duale Operatoren definiert, ändert sich die Zuwesung in der dritten Zeile in loc = op(loc, x[i]); .Natürlich muss der Operator vorher definiert worden sein.
Eine mathematische Funktion ist für Java-Programmierer nur eine Methode die einen typisierten Wert zurückgibt und mit einer Argumentliste aus typisierten Argumentvariablen. Für Mathematiker - die Leute für die MathML gedacht ist - gilt etwas anderes.
Funktion, eindeutige Abbildung von einer Menge X auf die Menge Y.
X heißt Urbildmenge oder Definitionsbereich D
Y heißt Bildmenge oder Wertebereich W
Jedem Element
wird
in eindeutiger Weise ein Element
zugeordnet.
Etwas übersichtlicher mag die allgemeine Schreibweise dieser Zusammenhänge sein. Geben sie doch Auskunft über die unbedingt anzugebenden Mengen oder Bereiche.
Weil x ein Element aus der Menge
X ist und diese Menge der Definitionsbereich ist, ist die
Angabe dieser Menge notwendig. Natürlich gibt es eine Ausnahme;
wenn
darf
diese Angabe fehlen.
Bereits
die Verwendung der Zahlenmenge
bereitet
Probleme, denn Computern ist diese Zahlenmenge nicht zugänglich.
Nun ist es aber allgemeine Praxis von real Typen zu sprechen, wenn
nicht ganzzahlige Werte gemeint sind. In Computern liegt immer nur
die Zahlenmenge
vor.
Auch natürliche Zahlen
sind
nicht ohne, denn es existieren (in Java) nur Werte aus
womit
ein Vorzeichen immer vorhanden ist.
In derartigen Fällen helfen nur Konventionen. So werden für Variablen folgende Typen mit entsprechenden Zahlenmengen assoziiert:
Werden spezielle Definitionsbereiche vereinbart, müssen sie mit speziellen Exceptions abgefangen werden. Durch die ausschließliche Verwendung von Objekten kann praktisch jeder Bereich definiert werden. Java stellt für diesen Zweck die Klasse Number bereit.
Die Definition einer Funktion ist bereits komplexer. Hier bieten sich wenigstens zwei Schreibweisen an, die auch gleichberechtigt unterstützt werden. zunächst muss der Funktionswert über den Wertebereich mit dem Typus assoziiert werden. Es sind also mindestens zwei Angaben zu Bereichen (Zahlenmengen) nötig, um eine Funktion zu definieren. Die folgenden Zeilen sind hinsichtlich des generierten Codes synonym und generieren den gleichen Code.
double f(double x) {
return a * x + b;
}
|
Hier zeigt sich bereits ein weiteres Problem. Die Konstanten mit den Bezeichnungen a und b sind nicht definiert. Auch diese Elemente müssen Mengen zugewiesen werden. Dabei ist die Reihenfolge zu beachten, die zuerst den Bereich und dann erst die Wertzuweisung verlangt.
double final a=2; double final b=0; |