MathML Grundlagen

Mathematiker gelten gemeinhin als sonderbare Leute, besonders was die Programmierung betrifft. Schnell skizzieren sie die umfangreichsten Formelgebilde und sprechen dann von einem gelösten Problem. Beispielhaft dürfte folgendes Szenario sein.

Gefragt nach einem Verfahren zur Ermittlung der größten gemeinsamen Teilers (ggT) kam die Antwort:

Sie bilden die Schnittmenge der beteiligten Teilermengen und bestimmen das maximale Element.

An Minimalismus kaum zu unterbieten, allerdings ohne Bezug zur programmtechnischen Umsetzung. Die Bestimmung der Teilermenge von 12¹² sei hier als Herausforderung genannt.

Formulierung in MathML

Jeder mathematische Ausdruck kann in eine Struktur zweier Operanden und einen Operator zerlegt werden. Die dabei gemachten stillschweigenden Voraussetzungen sind für programmierende Informatiker oft in Vergessenheit geraten. So basiert selbst die Anwendung des unären Minus-Operators auf der Anwendung des neutralen Elements für Addition der zugrunde liegenden Zahlenmenge. So bedeutet -5 eben (0 - 5) für alle eindimensionalen Zahlenmengen.

Diese Tatsache nutzt MathML und bietet gleichzeitig eine extrem hohe Flexibilität. Zwischen Operatoren und Operanden wird streng unterschieden. Auch Zahlen und Identifier werden getrennt. Ein Beispiel:

x = 4 + 5

in MathML formuliert

<mi>x</mi><mo>=</mo><mn>4</mn><mo>+</mo><mn>5</mn>

Die verwendeten Tags bedeuten: mi = Identifier, mo = Operator und mn = Number. Eine erste Beschreibung der Tags findet sich im Abschnitt "MathML Elemente".

Die zweifellos jetzt zuerst gestellt Frage wird die unären Operatoren betreffen und gleich folgend wird sie um die allgegenwärtigen binären Struktur erweitert. Deshalb gleich ein erweitertes Beispiel:

x = (4 + 5) / -2

in MathML formuliert

<mi>x</mi><mo>=</mo>
               <mfrac>
                <mrow>
                 </mo><mn>4</mn><mo>+</mo><mn>5</mn>
                </mrow>
                <mn>-2</mn>
               </mfrac>

Das Tag mfrac meint einen Bruch und erfordert exakt zwei Operanden. Der Zähler des Bruchs kann in Klammern gesetzt werden, wenn der gesamte Ausdruck mathematisch korrekt dargestellt wird, muss aber nicht. MathML stellt für diesen Fall das mrow-Tag zur Verfügung, welches die enthaltenen Elemente zu einem kapselt. Das mfrac-Tag kapselt seinerseits Zähler und Nenner des Bruchs, womit der "="-Operator ebenfalls binär wird.

Der unäre Operator des Nenners ist ein rein mathematisches Problem. Wird die Hierarchie der Zahlenmenge oberhalb der Menge

angelegt, handelt es sich um einen negativen Wert. Damit ist mindestens die Mengevorhanden, in der ja die Zeichenfolge "-2" bewertbar ist. Genau hier liegt ein Aspekt der Flexibilität von MathML, denn ob bewertbare Zeichenfolgen vorliegen oder nicht, ist eine Frage der "stillschweigend" gemachten Voraussetzungen. Die Zeichenfolge "-2" ist hier als Zahl vereinbart, womit eine Auswertung sehr erleichtert wird. Natürlich könnte der unäre Operator auch in ein mo-Tag eingebettet werden, aber dann wäre der unmittelbare Bezug zur Zahlenmenge nicht mehr vorhanden.

Die Tags von MathML haben mehr mathematischen Charakter denn typografischen. Diese Tatsache hilft sehr, wenn es an die Umsetzung von MathML-Sequenzen in Programme geht.

Struktur der Speicherung

MathML ist XML. Es ist also prinzipiell möglich, die herkömmlichen Parse-Konzepte (DOM-, SAX-Parsing) auch für MathML zu benutzen. Hier wird das SAX-Parsing verwendet, weil eine eigene Speicherstruktur (nicht DOM) zum Einsatz kommt. Diese Entscheidung fiel, weil das System auch für Ausbildungszwecke entwickelt wurde und die Programmierung von Baumstrukturen nun einmal dazugehört. Natürlich wird im Abschnitt "MathML darstellen" das List Processing von Java verwendet.

Ein Ausdruck wird benötigt und er sollte nicht zu einfach sein.

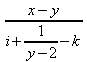
Seine Formulierung in MathML lautet:

<?xml version="1.0" encoding="iso-8859-1"?>
<math xmlns="http://www.w3.org/1998/Math/MathML">
 <mfrac>
  <mrow>
   <mi>x</mi>
   <mo>-</mo>
   <mi>y</mi>
  </mrow>
  <mrow>
   <mi>i</mi>
   <mo>+</mo>
   <mrow>
    <mfrac>
     <mn>1</mn>
     <mrow>
      <mi>y</mi>
      <mo>-</mo>
      <mn>2</mn>
     </mrow>
    </mfrac>
   </mrow>
   <mo>-</mo>
   <mi>k</mi>
  </mrow>
 </mfrac>
</math>

Mit jedem MathML fähigen Browser (z.B. Amaya) kann diese Sequenz aus der Datei math1.xml angezeigt werden. Jetzt sollen jedoch die Elemente des Ausdrucks in einer Struktur abgelegt werden, um dann mit eigenen Programmen weiterverarbeitet zu werden.

Wie so häufig bei Sprachen, liegt auch hier eine rekursive Bearbeitung nahe, womit zunächst ein Speicherelement für verkettete Organisation benötigt wird.

Ein MathML-Node

Dieses Speicherelement muss mindestens über je eine Referenz zum eigenen Vorgänger und Nachfolger verfügen. Zwei weitere Referenzen helfen bei der späteren Arbeit; es ist eine Referenz zu Kind-Knoten und eine zum eigenen Elter-Knoten. Natürlich darf auch der eigene Inhalt nicht fehlen. Letzterer sollte am Anfang eines Projekts sehr allgemein gehalten werden.

public class Node {
public Object object; // Inhalt des Nodes
public Node   parent; // Referenz auf übergeordneten Node
public Node   child;  // Referenz auf untergeordneten Node
public Node   prev;   // Vorgänger
public Node   next;   // Nachfolger

 public Node() {
  object = null;
  parent = null;
  child  = null;
  prev   = null;
  next   = null;
 }
}

Aus vielen dieser Nodes soll nun ein Baum aufgebaut werden. Dabei müssen die Inhalte der Nodes natürlich den Inhalten der Tags entsprechen. Damit stehen die beiden Aufgaben des Parsers fest; es sind Aufbau des Baums und Übernahme der Inhalte.

Ein erster MathML-Parser

Der SAX-Parser stellt über seinen DefaultHandler die wichtigsten Methoden bereit. Nicht einmal um deren Koordinierung braucht sich der Entwickler Gedanken zu machen, wohl aber über ihre Tätigkeiten. Deshalb zunächst einmal die Aufgaben der Methoden und dann deren Tätigkeiten.

startDocument
wird aufgerufen, wenn der Parser den Start eines XML-Dokuments erkennt.
endDocument
wird aufgerufen, wenn der Parser das Ende eines XML-Dokuments erkennt.
startElement
wird aufgerufen, wenn der Parser den Start eines Tags erkennt.
endElement
wird aufgerufen, wenn der Parser das Ende eines Tags erkennt.
characters
wird aufgerufen, wenn der Parser textuellen Inhalt erkennt.

Die ersten Schritte beschäftigen sich nicht mit NameSpacing und attributierten MathML-Tags, weshalb die entsprechenden Parameter der Methoden einfach ignoriert werden. Wichtig sind im Augenblick nur Tags und textueller Inhalt. Weil die Inhalte der gelieferten Daten kaum bekannt sind, werden sie bezeichnet und in eckige Klammern gefasst.

Die Anzeige der wesentlichen Daten eines einleitenden Tags:

 public void startElement( String uri, String local, String tag, Attributes attrs) {
  if (tag != null) System.out.println( "start-tag=["+tag+"]");
 }

Die Anzeige der wesentlichen Daten eines beendenden Tags:

 public void endElement( String uri, String local, String tag) {
  if (tag != null) System.out.println( "end-tag=["+tag+"]");
 }

Die Anzeige aller isolierten Zeichen zwischen Start- und End-Tag::

 public void characters( char[] ch, int start, int length) {
 String str = new String( ch, start, length);
  if( str != null) System.out.println( length+" Zeichen ab Position "+start+" isoliert: ["+str+"]");
 }

Diese Methoden verrichten ihre Arbeit chronologisch zwischen den Methoden

 public void startDocument() {
  System.out.println( "Anfang des Dokuments");
 }

und

 public void endDocument() {
  System.out.println( "Ende des Dokuments");
 }

Koordiniert werden die Abläufe einzig von dem SAX-Parser. Sein Aufruf erfolgt hier in der main-Methode, die auch wegen der zu behandelnden Exceptions die umfangreichste ist.

 static public void main( String[] args) {
 DefaultHandler handler = new parsen1();
 File           file    = new File( "math1.xml");

  if   (file.canRead())
       {
        try   {
              SAXParserFactory factory = SAXParserFactory.newInstance();
              SAXParser        parser  = factory.newSAXParser();

               parser.parse( file, handler);
              }
        catch (Throwable t)
              {
               t.printStackTrace();
              }
       }
  else {
        System.out.println( "Datei ist unbekannt.");
        System.exit( 1);
       }
 }

Das Ergebnis der bisherigen Bemühungen ist mit dem Begriff "kläglich" noch sehr positiv umschrieben, denn sollte das Programm "parsen1.java" gestartet werden, ergibt sich folgendes Ergebnis (nur auszugsweise dargestellt):

Anfang des Dokuments
start-tag=[math]
0 Zeichen ab Position 94 isoliert: []
1 Zeichen ab Position 0 isoliert: [
]
1 Zeichen ab Position 96 isoliert: [ ]
start-tag=[mfrac]
0 Zeichen ab Position 104 isoliert: []
1 Zeichen ab Position 0 isoliert: [
]
2 Zeichen ab Position 106 isoliert: [  ]

Offensichtlich interpretiert der SAX-Parser Zeilenende-Kennungen als Delimiter und beginnt einen neuen Lauf der Zeichenauslesung. Wehalb hier auch keine Zeichen als Zeichenfolge übergeben werden ist weitgehend unbekannt. Es ist zwar möglich, den Parser mit den zu ignorierenden Zeichen auszustatten, aber die API-Documentation von Java rät ausdrücklich davon ab. Vom Nutzen für den Anwender entspricht dieser Parser der Ackermann-Funktion.

Isolation der relevanten Inhalte

Es sollen hier auch die relevanten Zeichen mit den Tags in die Baumstruktur übernommen werden. deshalb werden die entsprechenden Methoden und Referenzen zur Speicherverwaltung hinzugenommen,

Um überhaupt in einer Baumstruktur navigieren zu können, muss die Wurzel (root) bekannt sein. Hilfreich ist auch, die Spitze des Baums (letzer Node) zu kennen. Wenn ein Baum wächst muss der Ort des Wachstums bekannt sein. Ein neuer Zweig unterscheidet sich erheblich vom Wachstum des Stamms. Die Unterscheidung übernimmt eine Boolesche Variable.

Node    root   = null;  // erster  Node im Baum
Node    last   = null;  // letzter Node im Baum
boolean append = false; // anhängen oder einfügen

Wichtig ist die Einbringung neuer Knoten in die Baumstruktur. Für diesen Zweck ist eine separate Methode vorhanden, die einen neuen Node entweder an den vorhandenen Zweig anhängt, oder einen neuen Trieb (child) an den vorhandenen anlegt.

 public void insert( String str) {
 Node node = new Node();

  node.object = str;
  if   (root == null)
        root  = node; // einziger Node ist Wurzel
  else {
        if   (append)
             last.next   = node; // Node ist Nachfolger
        else last.child  = node; // Node ist ChildNode
        node.parent = last;      // Node hat Last als Elter
       }
  last = node; // Neuer ist Letzter
 }

Das steuernde Element ist die Variable append (hier rot hevorgehoben). Diese variable wird von den Methoden start-, endElement entsprechend gesetzt. Diese Methode hat als Argument keinen Node, sondern nur einen String. Dieser besteht aus relevanten Zeichen und wird erst hier als Inhalt in einen neuen Node übernommen. Letzterer wird in den Baum integriert.

Handelt es sich bei dem zu integrierenden Node um den ersten, so ist der Zustand der variable append ohne Belang. In diesem Fall ist der neue Node auch der einzige und damit sowohl erster (root) als auch letzter (last).

Die umfangreichste Änderung erfährt die Methode characters, denn hier müssen die relevanten Zeichen für den Inhalt isoliert werden. Deshalb wird diese Methode zuerst besprochen.

 public void characters( char[] ch, int start, int length) {
 String str = new String( ch, start, length);

  str = str.trim();
  if (str.length() < 1) return;
  System.out.println( "["+str+"]");
  insert( str);
 }

Die Metode trim aus der Klasse String übernimmt die Hauptarbeit. Besteht der String nur aus white spaces, werden diese entfernt und die Länge ist 0. Wenn der String über keine Zeichen verfügt, wird die Methode einfach verlassen. sind jedoch Zeichen vorhanden, handelt es sich um relevante Zeichen, die in den Baum integriert werden. Diese Aufgabe übernimmt die Methode insert. Zeichenfolgen sind somit immer direkt mit einem einleitenden Tag verbunden, wofür jedoch die entsprechende Methode sorgt.

 public void startElement( String uri, String local, String tag, Attributes attrs) {
  System.out.println( "Start "+tag);
  insert( tag);
  append = false;
 }

Die steuernde Variable append wird auf false gesetzt, denn einleitende Tags besitzen in diesem Modell immer mindestens einen untergeordneten Knoten (child). Einleitende Tgs sind natürlich immer relevant, weshalb sie auch ind den Baum integriert werden. Daraus folgt auch, dass die nächste zur Anwendung kommende Methode characters ist und die relevanten Zeichen in einem untergeordneten Zweig gespeichert werden.

Nachdem die Zeichenfolge(n) übernommen wurde(n) kommt in einem korrekten XML-Dokument ein End-Tag. Die entsprechende Methode

 public void endElement( String uri, String local, String tag) {
  System.out.println( "End   "+tag);
  last   = last.parent;
  append = true;
 }

setzt zunächst die Spitze des Baums (last) auf den letzten Node des Elter-Zweigs. Damit wird ein folgendes Anhängen von Nodes am Elterntweig stattfinden. Unmittelbar folgend wird append auf true gesetzt, denn jetzt folgende relevante Zeichen sind Bestandteil dieses Zweiges. Die Zeichen dieses End-Tags sind irrelevant, denn sie entsprechen dem Start-Tag.

Um das Ergebnis zu überprüfen, fehlt noch eine Methode zur Ausgabe. Es handelt sich um eine rekursive Methode, denn die Strukturen können so am besten bearbeitet werden.

 static public void showTree( Node node, int level) {
  if (node == null) return;
  for (int i=0; i < level; i++)
       System.out.print( " ");
  System.out.println( (String)node.object);
  showTree( node.child, level+1);
  showTree( node.next,  level);
 }

Damit auch die Rekursionstiefe angezeigt wird, werden entsprechend viele führende Leerzeichen ausgegeben. und erst dann der Inhalt des Nodes. Ist der Node selbst eine Nullreferenz, kehrt die Methode sofort in die aufrufende Ebene zurück.

Der unschätzbare Vorteil dieser Vorgehensweise ist die Möglichkeit verschiedene Notationen zu erzeugen. So kann die Ausgabe in prefix- oder in postfix-Notation erfolgen, ohne Wesentliches an der Methode zu ändern. Die folgende Sequenz zeigt die entsprechende Änderung:

 static public void showTree( Node node, int level) {
  if (node == null) return;
/*
  for (int i=0; i < level; i++)
       System.out.print( " ");
  System.out.println( (String)node.object);                               
*/
  showTree( node.child, level+1);

  for (int i=0; i < level; i++)
       System.out.print( " ");
  System.out.println( (String)node.object);

  showTree( node.next,  level);
 }

Die jeweils gelieferten Ergebnisse sind:

prefix	postfix
math mfrac mrow mi x mo - mrow mi i mo + mrow mfrac mn 1 mrow mi y mo - mn 2 mo - mi k	x mi - mo i mi + mo 1 mn y mi - mo 2 mn mrow - mo k mi mfrac mrow mrow mrow mfrac math

Natürlich wird diese Methode um ein entsprechendes Argument erweitert, wenn tatsächlich von beiden Notationen Gebauch gemacht werden sollte.

Es fehlt nur noch der Aufruf, den Inhalt des Baums darzustellen. Es genügt, die beiden folgenden Zeilen an die bislang letzte Zeile der main-Methode anzuhängen.

  System.out.println( "\n\nSAX-Parsing abgeschlossen, anzeigen des Baums:");
  showTree( ((parsen2)handler).root, 0);

Das gesamte Programm ist unter "parsen2.java" zu finden.